プロジェクト

【種々の海底地形における津波の伝播（理学部情報科学科　河村研究室）】

津波は地震・火山による災害と並び、規模や被害が大きな自然災害です。 近年では、2004年のスマトラ島沖地震に伴う大津波などが、まだ記憶に新しいことと思います。 そこで本研究では、海底地形の差による津波の伝播に着目し、 その違いを三次元計算で解析を行いました。
また、津波と地震波には類似性があり 海と柔らかい地盤、海底と固い地盤と対応付けられるので 地形のモデルとして阪神（阪神大震災）とサンフランシスコ（ロマプリータ地震）での地震のデータを用いることにしました。

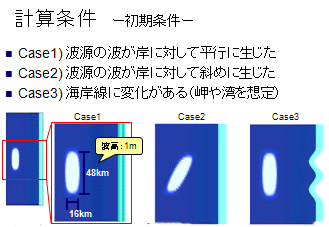計算条件としては、以下の3つの場合で初期条件を設定し比較を行いました。 Case1、 Case2、 Case3です。
この時の波源の大きさは16km×48kmで、波高は1メートルと想定しました。
また、地震により海底が隆起して波が発生した状況を想定しているので、 この波源は強制的に振動はさせません。

下の三つの動画はCase1の平行の場合です。 色は波の高さを表していて、白いほど高く、青が濃いほど低いことを表しています。 波の伝播する形と岸側の境界面に注目してください。
１．同じスピードで広がり、右の境界では岸から沖へ向かう綺麗な反射の様子が見て取れます。
２．こちらは徐々に岸に近づくにつれて波が高くなっているのが分かります。
３．海底地形の一つ目の山で波が増幅していることと次の谷では急激に波高が減少していることが分かります。

　 ムービーを見るにはWindows Media Playerが必要です。
　

次にCase2の波源の波が斜めの場合の動画です。
１．平面の場合は初期の波の形から同心円状に広がっている様子が見て取れます。
２．阪神型の場合では浅くなるにつれて岸に平行に波が立っていく様子が見て取れます。
３．サンフランシスコ型の場合では、まずは最初の浅くなっている部分に向けて波が平行になりますが、 その後また深くなるので、この部分でスピードがまた速くなる分若干波が歪んで岸側に到達するように見えます。 この結果をまとめると、 海底地形の変化が波に影響を与えていることが分かり、 また水深が浅くなるにつれて海岸線の形に変形していく波の性質を確認することができました。

　 ムービーを見るにはWindows Media Playerが必要です。
　

最後にCase3の結果です。岸側に注目してご覧ください。
海側に出ている部分が岬を、引っ込んでいる部分が湾を想定しています。 地形に変化がある方がこの岬部分で波が高くなっていることが分かります。
これらの結果から、平面では岬部分での波の増幅が見られないことがわかります。 これは、グラフで比較しても一目瞭然で、 このグラフは各地形での岬の先端部、湾の中心部での波高の様子を表しているもので この太くなっている部分が平面地形の岬の先端部での波の振幅の様子です。 これを見て分かるように他の波に比べて波高と振幅が小さいことが分かります。 このことから、地形の変化が波に影響を与えていることが分かり、 波の屈折効果や流れ込む様子を確認できました。

　 ムービーを見るにはWindows Media Playerが必要です。

以下に計算方法を説明します。
X方向を沿岸に向かう方向、ｙ方向を鉛直方向とした三次元空間において 境界に沿った不等間隔格子を用いました。 格子数は65×21×51です。また領域の大きさは100km:4km:200kmを想定しています。 遠浅の地形として阪神の地形、起伏のある地形としてサンフランシスコの地形の2種類を 平面の地形との比較の対象といたしました。 それぞれの地形を以降、阪神型、サンフランシスコ型と呼ぶことにします。

次に計算に用いる基礎方程式ですが、 本研究では以下の連続の式と非圧縮性ナビエ・ストークスの方程式を用い、 これをMAC法で計算しました。 各係数は上のように設定しています。

また、境界条件は 表面は海面を想定しているので、時間で位置が変化する自由表面を、 底面は海底としているので固定、 また、この３つの側面は滑り壁条件（FSBC）を用いますが、 反射波の影響を考慮し、遠洋側の面は流出境界条件を用いることにしました。 この境界条件の係数 Uc には様々な決定法があります。 そこで、まず前段階として 本研究で用いる計算領域に最も適する条件を検証しました。

今回用いる流出境界条件は以下の式で与えられる 有限差分法に対する流出境界条件の 1つ である Sommerfeld 放射条件です。 ここで、この係数Ucは流出境界における法線方向の零でない“適当な“対流速度であり、 先ほど述べましたようにその決定法には様々なものがあります。 本研究では次の２つの場合、一様流速度とする場合と 流出境界における法線方向速度の最大値と最小値の算術平均値を用いた場合で比較を行いました。
また、領域内への流れ込みを制御する条件として以下の 6つ の制約で検討しました。 簡単に説明すると、法線方向成分にのみのものと各ベクトル成分に対するものがあり、 例えば、これは「速度が内側を向いたらゼロにする」や「速度が一つ内側の向きと違う場合はゼロにする」 といった条件です。
さらに、境界のベクトルに対して、このSRCを使用するのではなく法線方向速度にのみ適用させた場合も合わせ全部で 20 通りの検討を行いました。

流出入の制約の有無は動きの誤差にかかわる部分なので後で触れることとし、ここでは、ベクトルでUc＝１の時の結果を例にとして見ていくことにます。
このグラフは領域内のある地点（つまり格子）での高さの時間変化のグラフです。 場所としては、右図の対応する３点を比較しており、実線が２倍の領域のもの、破線がSRCを用いたものです。 実線の振る舞いにより近いものが条件として適切であると考えました。
実際にグラフを見てみると…緑が境界上での振る舞いですが、 波の山は上手く流れ出ていますが、谷の方は下がりすぎ…波が増幅されていることが見て取れます。 この影響により他の場所でも途中から振る舞いが乱れてしまいました。
同様にして、他の場合も比較したものをまとめると次のようになりました。 ベクトルで平均をとったものは全く変な動きになってしまい、 法線方向のみの場合はUc=1の時は波の山も半分反射してしまい、 平均をとったものは自由端反射と同じ振る舞いをするという結果が得られました。
ですので、今回はこのベクトルでUc=1の場合を用いることとし、 次に流れ込みの制約による違いをみていきます。

これらのグラフは３地点での高さの時間変化のグラフになります。
AからDの差はどれも似た振る舞いをしており、時間が経つにつれ、ある高さに落ち着く様子が見て取れますが Eでは水面が上昇傾向、Fでは水面が下降傾向にあることが分かりました。
そこで、今回は一番振る舞いが落ち着いていて、 中でも誤差の小さかったDの条件を用いることとしました。
このように境界条件を決定しています。

プロジェクトトップページに戻る

　

Copyright (C) 2011-2014 お茶の水女子大学シミュレーション科学教育研究センター, All rights reserved.