プロジェクト
【拡散に付随したモンテカルロ・シミュレーションの理論と応用に関する研究
(吉田裕亮・桑田和正・小林由香)】
本研究課題においては、自然現象・社会現象など多くの現象に現れる基本的な運動のひとつである拡散に関するその数理科学的な研究を中心に行いました。 単純な拡散は単にラプラス項のみからなる熱伝導方程式で記述できますが、一般の拡散方程式にはドリフト項が存在します。 ドリフト項はもちろん空間の位置に依存するが、このドリフト項が時間にも依存する拡散過程を記述する変数係数の偏微分方程式に基づく数値計算が必要となり、 計算格子(メッシュ)が細かくなると、厳密な時間発展の予測にはかなりの計算コストを要します。 そこでドリフト項を取り込んだ確率微分方程式に基づくモンテカルロ法による近似解の計算は十分に意味を持ちます。 本研究では、この拡散過程を記述する確率微分方程式に付随したモンテカルロ・シミュレーションの基礎研究ならびに、拡散方程式と確率分布間距離の理論を中心に、 近年注目されているWasserstein距離と最適輸送理論の関連に関する調査研究を目的としました。
ポテンシャル関数Vによる拡散を記述する偏微分方程式は、
(1) 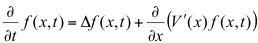
で与えられる。ここで、Δはラプラシアンで、関数Vについて、時間には依存せず、空間にのみ依存するポテンシャルとします。
この微分方程式の解f(x,t)は拡散物質の密度を表すことになります。
この微分方程式はFokker-Planck方程式と呼ばれ、拡散現象における基本方程式です。
この編微分方程式に対応する、拡散現象を記述する確率微分方程式は
(2) 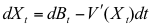
で与えられられます。ここでBtはブラウン運動です。
(1)の定常状態、すなわち(2)式の時間無限大に対応する確率変数X∞の従う確率分布は、初期分布(X0の分布)の取り方に依らずポテンシャルVのGibbs分布
(3) 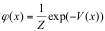
として与えられます。
本課題の研究目的のひとつとしたGibbs分布への収束の速さに関する調査研究については以下のような結果を得ました。 時刻tの確率課程Xtの確率分布とGibbs分布の距離をWasserstein 2-distanceで議論しました。 一般に、パラメトリックな族からなる確率分布のなす多様体で、2つの確率分布を比較することは、情報幾何の基本です。 情報幾何では、Kullback-Leibler距離 (相対エントロピー)を用いての議論が多いのですが、Kullback-Leibler距離は、擬距離であり、また後に述べるように、輸送コスト不等式からWasserstein距離の方が 強い意味での収束を意味することより、Wasserstein距離に関しての議論の方が汎用的です。
Wasserstein距離のdissipation公式から収束は指数オーダであり、収束の速度はポテンシャル関数Vの凸性、すなわち2階微分により決定されることは、既に知られていますが、 このdissipation公式を精査することにより、輸送コスト不等式が導出されることが確認されました。 このことは輸送コスト不等式(相対エントロピー擬距離がWasserstein距離を上から評価可能であるとの不等式)は、実は収束のオーダも保存するものであり、これら2つの量の最良の不等式であることが分かります。 この結果に関しては、報告書作成時の現在、大学院理学専攻の院生と共に学術雑誌への投稿に向けて取り纏めを行っています。
更に、本研究課題においては、ランダム行列、行列値の確率過程と関連で最近研究がなされているMcKean-Vlasov方程式に関して、Fokker-Planck方程式と同じように時間発展で分布が記述される場合に関して、 輸送コスト不等式、対数Sobolev不等式ならびに定常分布への収束に関する調査研究も行いました。
まず、McKean-Vlasov方程式とは、
(4) 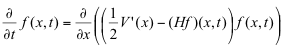
と与えられる非線形な偏微分方程式です。
ここでHfはfのHilbert変換です。このPDEは(1)のFokker-Planck方程式と類似の形式を有するものです。実際、PDE(1)は
(5) 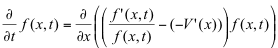
と変形されます。すなわち、空間微分側にスコアー関数の差に密度fが掛った形式をしています。
自由確率論においては、密度関数のスコアー関数がヒルベルト変換で与えられるので(4)の空間微分側に、ちょうどスコアー関数の差が現れることになっています。
このMcKean-Vlasov方程式についても、自由エントロピーのdissipation公式を導くことにより、対数Soblev不等式ならびに輸送コスト不等式を示すことを行いました。 さらに、収束の速さに関しても、通常の確率論と同じく指数オーダでの収束を行うことが示されました。 このMcKean-Vlasov方程式に関してのこれら一連の結果に関しても大学院理学専攻の学生と成果の取りまとめを行っています。
次に、行列値の拡散過程に関するシミュレーションとしてランダム行列を用いた統計的データ解析への応用に関する研究も行いました。 特に、本課題においては時系列データの解析にランダム行列を用いる手法に関して大きな進展が得られました。 具体的にはMAモデル表現される時系列データに関しては、そのモデルの評価に関してランダム行列を経由してMachenko-Pastur分布と類似の分布に対応させて評価式を導出することを行いました。 MAモデルで表現される離散Gausss過程について、それらデータから行方向に順に並べることにより十分に大きな行列Xを作り、これをデータ行列として共分散行列Dを考えます。 これは、一般に行方向に相関のあるランダム行列Xの共分散行列を考えたことになります。 このようなタイプのランダム行列のスペクトル解析に関して最近出版された論文を精査したところ、データから定まる共分散行列DのスペクトルのモーメントとMAパラメータから定まるパラメータ行列 Hのモーメントの間には自由複合Poisson分布としての関係があることが導かれました。 これにより、データからの共分散行列からパラメータ行列のスペクトル分布のモーメントが推定可能となり、パラメータ推定の良さの基準を構成することが可能となりました。 十分に大きなデータを用いてのシミュレーションにおいてもかなりの精度で事前に設定したパラメータから定まるパラメータ行列のスペクトル分布のモーメントも復元できることも確認されました。
この結果は、既に最近出版された論文の結果についての別証明も与えることになり、昨年度末に取りまとめを行い学術雑誌への投稿を行いました。 報告書作成時において、当該論文の査読結果として修正の上での掲載が認められるとの状態にあります。
以上が、本研究課題の成果の概略です。 本研究グループとしては、研究計画に沿ってのほぼ研究目的に合った成果が得られたものであると考えています。 また、貴センター学内科研で配分頂いた研究費は、研究代表者・分担者ならびに大学院理学専攻の学生研究協力者の成果発表ならびに関連書籍の購入と、有効に活用させて貰ったことも併せてご報告します。
学術論文
- Gigli, N., Kuwada, K. and Ohta, S. "Heat flow on Alexandrov spaces" Communications on Pure and Applied Mathematics Vol. 66, no.5 (2013) 307-331.
- Hirata, M., Nemoto. A., and Yoshida, H. "An Integral Representation of the Relative Entropy" Entropy Vol.14, no.8 (2012) 1469-1477.
- Kuwada, K. "Convergence of time-inhomogeneous geodesic random walks and its application to coupling methods" Annals of Probability Vol. 40, no. 5 (2012) 1945-1979.
研究発表
- 川久保 秀子, 吉田裕亮, “カーネル法とランダム行列理論によるノイズ変数の除去”, 電子情報通信学会 情報論的学習理論と機械学習研究会 (IBISML), 名古屋工業大学, Nagoya, Japan, 2013年3月5日.
- 川久保 秀子, 吉田裕亮, “ヒルベルト-シュミット独立基準に基づくノイズ変数の除去”, 情報処理学会 MPS=BIO研究会, 京都大学, Kyoto, Japan, 2012年12月7日.
- 北口景子, 吉田裕亮, “カーネル法によるDP-means法の非線形化”, 情報処理学会 MPS=BIO研究会, 京都大学, Kyoto, Japan, 2012年12月7日.
- Kuwada, K., "Wasserstein contractions associated with the curvature-dimension condition", ERC Workshop on Optimal Transportation and Applications, Scuola Normale Superiore, Pisa, Italy, 2012年11月9日.
- Kuwada.K, "熱分布の結合法と次元曲率条件", 日本数学会 2012年度秋期総合分科会 統計数学分科会 特別講演, 九州大学, Fukuoka, Japan, 2012年9月18日.